Feeling acceleration (Rindler spacetime)

This is the first article of a series on the Unruh effect. The final aim is to discuss a new paper on which I am working with the ICFO guys, about a proposal for a quantum simulator to demonstrate how those things work. We are going to discuss some rather tough stuff: Rindler spacetime, quantum field theory in curved spacetime, Hawking radiation, inversion of statistics… and it gets mixed with all the funny stories of cold atoms in optical lattices. I’ll do my best to focus on the conceptual issues, leaving all the technicalities behind.

Our journey starts with special relativity. Remember Minkowski spacetime diagrams? The horizontal axis is space, the vertical one is time. The next figure depicts a particle undergoing constant acceleration rightwards. As time goes to infinity, the velocity approaches c, which is the diagonal line. But also, as time goes to minus infinity, the velocity approaches -c. We’ve arranged things so that, at time t=0, the particle is at x=1.

Minkowski diagram of an accelerated particle.

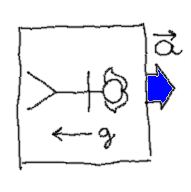
Now we are told that the particle is, really, a vehicle carrying our friend Alice inside. Since the real acceleration points rightwards, she feels a leftwards uniform gravity field. Her floor, therefore, is the left wall.

Alice in her left. Acceleration points rightwards, “gravity” points leftwards.

Are you ready for a nice paradox? This one is called Bell’s spaceship paradox. Now, imagine that Bob is also travelling with the same acceleration as Alice, but starting a bit behind her. Their trajectories can be seen in the figure

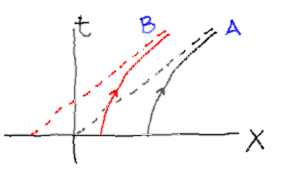
Alice and Bob travel with the same acceleration. Their distance, from our point of view, is constant.

From our point of view, they travel in parallel, their distance stays constant through time. So, we could have joined them with a rigid bar from the beginning. Wait, something weird happens now. As they gain speed, the rod shrinks for you… This is one of those typical paradoxes from special relativity, which only appear to be so because we don’t take into account that space and time measures depend on the point of view. This paradox is readily solved when we realize that, from Alice’s point of view, Bob lags behind! So, in order to keep up with her, and keep the distance constant, Bob should accelerate faster than her!

So, let us now shift to Alice’s point of view. Objects at a fixed location at her left move with higher acceleration than she does, and objects at her right move with lower acceleration. Her world must be pretty strange. How does physics look to her?

One of the fascinating things about general relativity is how it can be brought smoothly from special relativity when considering accelerating observers. In order to describe gravity, general relativity uses the concept of curved spacetime. In order to describe how Alice feels the world around her we can also use the concept of curved spacetime. It’s only logical, Mr Spock, since the principle of equivalence states that you can not distinguish acceleration from a (local) gravity field.

Fermi and Walker explained how to find the curved spacetime which describes how any accelerated observer feels space around her, no matter how complicated her trajectory is. The case of Alice is specially simple, but will serve as an illustration.

The basic idea is that of tetrad, the set of four vectors which, at each point, define the local reference frame. In German, they call them “vier-bein”, four-legs, which sounds nerdier. Look at the next figure. At any moment, Alice’s trajectory is described by a velocity 4-vector v. Any particle, it its own reference frame, has a velocity 4-vector (1,0,0,0). Therefore, we define Alice’s time-vector as v. What happens with space-vectors? They must be rotated so that the speed of light at her point is preserved. So, if the time-vector rotates a given angle, the space-vector rotates the same vector in the opposite direction, so the bisector stays fixed.

The local frames of reference for Alice, at two different times.

Now, each point can be given a different set of “Alice coordinates”, according to local time and local space from Alice point of view. But this change of coordinates is non-linear, and does funny things. The first problem appears when we realize that the space-like lines cross at a certain point! What can this mean? That it makes no sense to use this system of coordinates beyond that point. That point must be, somehow, special.

In fact, events at the left of the intersection point can not affect Alice in any way! In order to see why, just consider that, from our point of view, a light-ray emmited there will not intersect Alice’s trajectory. Everything at the left of the critical point is lost forever to her. Does this sound familiar? It should be: it is similar to the event horizon of a black hole.

Red: what Alice can’t see. Green: where Alice can’t be seen.

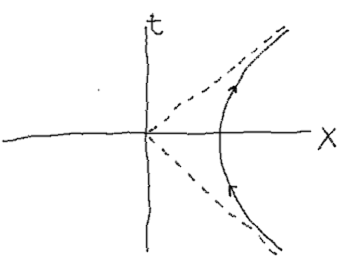
Let us assume that you did all the math in order to find out how does spacetime look to Alice. The result is called Rindler spacetime, described by the so-called Rindler metric. In case you see it around, it looks like this

Don’t worry if you don’t really know what that means. Long story short: when Alice looks at points at her left (remember, gravity points leftwards), she sees a lower speed of light. Is that even possible? That is against the principle of relativity, isn’t it? No! The principle of relativity talks about inertial observers. Alice is not.

So, again: points at her left have lower speeds of light. Therefore, relativistic effects are “more notorious”. Even worse: as you move leftwards, this “local speed of light” decreases more and more… until it reaches zero! Exactly at the “special point”, where Alice coordinates behaved badly. What happens there? It’s an horizon! Where time stood still.

The world for Alice, Rindler spacetime: speed of light depends on position, and becomes zero at the horizon.

Imagine that Alice drops a ball, just opening her hand. It “falls” leftwards with acceleration. OK, OK, it’s really Alice leaving it behind, but we’re describing things from her point of view. Now imagine that Bob is inside the ball, trying to describe his experiences to Alice. Bob just feels normal, from his point of view… he’s just an inertial observer. But Alice sees Bob talking more and more slowly, as he approaches the horizon. Then, he friezes at that point. Less and less photons arrive, and they are highly redshifted (they lose energy), because they had to climb up against the gravitational potential. Finally, he becomes too dim to be recognized, and Alice loses sight of him.

That description would go, exactly, for somebody staying fixed near a black hole dropping a ball inside it. The event horizons are really similar. In both cases, the observer is accelerated: you must feel an acceleration in order to stay fixed near a black hole! As Wheeler used to say, the problem of weight is not a problem of gravitation. Gravitation only explains free fall. The problem of weight is a problem in solid state physics!!

For more information, see Misner, Thorne and Wheeler’s Gravitation, chapter 6. It’s a classic. I wish to thank Alessio, Jarek and Silvia for suffering my process of understanding…

Advertisement